CDQ分治
2025-08-22 19:10:29 # code

前置知识点：分治（归并排序），树状数组

CDQ分治是一种强大的离线算法思想，由陈丹琦（cdq）在国家集训队论文中首次提出。其核心是将一个复杂的问题（通常是多维的、动态的）通过分治降维，分而治之。它最经典的应用是处理多维偏序问题，以及将一些动态问题转化为静态问题求解。

例题：三维偏序

P3810 【模板】三维偏序（陌上花开） - 洛谷

问题描述

有 n 个元素，第 i 个元素有 ai,bi,ci 三个属性。

定义一个函数 f(i)，它表示满足以下所有条件的元素 j 的数量：

  • aj ≤ ai
  • bj ≤ bi
  • cj ≤ ci
  • j != i

求解目标

对于 d∈[0,n) 的每个整数值，分别求出满足 f(i)=d 的 i 的数量。

分析

已知分治可以求逆序对，树状数组可以求逆序对，那么分治加树状数组呢？

可以求三维偏序。实际上就是两个求逆序对的方法结合。

乍一看感觉有点复杂，但我们可以通过降维将问题逐步简化。

假设我们现在有一组数据：

img

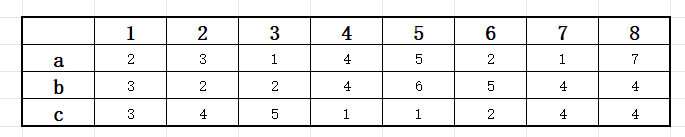
我们的大顺序按 a 属性的大小进行排序可以得到：

img

我们以4，5为边界将其划分为左区和右区，

一个元素 i 的最终答案 f(i)，其贡献来源于三个部分：

  1. 分治左区内部元素对左区元素的贡献。
  2. 分治右区内部元素对右区元素的贡献。
  3. 左区元素对右区元素的贡献。
1
2
3
4
5
6
7
8
9
void cdq(int l, int r)
{
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    cdq(l, mid);      // 左边去跑递归，完成左区内部贡献
    cdq(mid + 1, r);  // 右边去跑递归，完成右区内部贡献
    merge(l, mid, r); // 左右都跑完再进行左跨右贡献
}

我们可以通过递归去完成左区和右区内部贡献，那么现在关键就在于左跨右贡献要如何统计。

第一次降维：由于大顺序是按照 a 属性的大小进行排序的，所以我们可以知道右区内的所有元素的 a 属性都大于等于左区所有元素的 a 属性。至此，我们已经可以忽略 a 属性的影响，该问题简化为二维。

我们将左右区元素分别按照 b 属性进行排序。

img

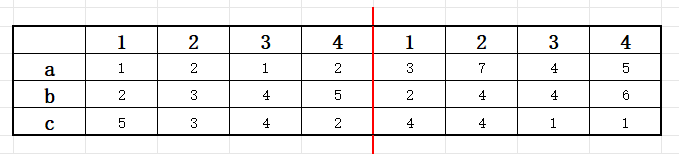
接着我们来遍历右区的每一个元素，寻找左区有多少元素能够对其产生贡献。

img

上面是树状数组的初始状态。现在 a 属性和 b 属性都处于有序状态了，我们用树状数组来记录 c 属性。

img

我们从左区寻找左区内 b 属性小于等于右区当前元素 b 属性的，可见左区内只有1号符合该条件，所以左区的指针移动到1号（初始为0号），注意，该挪动是不回退的，b 属性已经做好排序，随着右边元素遍历， 左区指针只会往后走。左区指针每次挪动时，我们用树状数组记录指针到达元素的 c 属性，此时树状数组状态应当如下。

img

第二次降维：由于左区指针所达位置及之前元素的 b 属性都小于等于右区当前元素，目前我们已经不用考虑 b 属性影响，该问题简化为一维。我们现在只需要考虑 c 属性。

统计左侧多少元素可以对右侧当前元素结果产生贡献，现在只用检查左区有多少元素 c 属性满足，那我们直接利用树状数组即可，右侧一号元素所加贡献为sum(4)（4为该元素的 c 属性值。我们继续遍历右侧元素。

img

遍历到右侧2号元素时，左侧指针可以挪动到3号，挪动过程中记录 c 属性值，目前树状数组的状态应当为

img

那么右侧2号元素所得到的贡献为sum(4),后面的遍历也是如此。遍历完右侧元素之后，我们已经完成了cdq分治中最重要的左跨右贡献。

这道题目还有一个小细节，如果有几个abc属性都相同的元素，他们应当是互相符合要求的，但是按照 a 属性排序以后，前面的元素是得不到后面元素的贡献的，所以我们需要进行一个预处理，提前将相同的元素加上后面应当有但是在分治中得不到的贡献。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 1e5 + 1;
int c[N];   // 树状数组
int f[N];   // 记录每个元素所得到的贡献
int ans[N]; // 储存答案
int n, k;   // n为元素个数，k为属性最大值
// 以下为树状数组函数
int lowbit(int x) { return x & -x; }
void add(int x, int y)
{
    for (int i = x; i <= k; i += lowbit(i))
        c[i] += y;
}
int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += c[i];
    return res;
}
// 我们用结构体来储存每个元素信息
struct aa
{
    int i, a, b, c;
    bool operator==(const aa &k) const
    {
        return (a == k.a && b == k.b && c == k.c);
    }
} a[N];
// 以a为第一关键字排序，若相同再按b，c进行排序，使得所有属性相同元素可以放在一起，便于提前加贡献
bool coma(const aa &a, const aa &b)
{
    if (a.a != b.a)
        return a.a < b.a;
    if (a.b != b.b)
        return a.b < b.b;
    return a.c < b.c;
}
// 按b排序
bool comb(const aa &a, const aa &b)
{
    return a.b < b.b;
}
// 左跨右贡献
void merge(int l, int mid, int r)
{
    //我们在上一层递归中已经将左右两个部分按照b属性排好序了，也就是该函数最后一行所做的事情
    int p = l - 1;                     // p为左区指针
    for (int i = mid + 1; i <= r; i++) // 遍历右侧元素
    {
        // 左区符合条件则挪动指针
        while (p + 1 <= mid && a[p + 1].b <= a[i].b)
        {
            p++;
            add(a[p].c, 1); // 树状数组记录c属性信息
        }
        f[a[i].i] += sum(a[i].c); // 右区当前元素得到贡献
    }
    // 注意，遍历完之后我们需要清空树状数组，撤销之前所记录的信息，避免其对其他分支产生影响
    for (int i = l; i <= p; i++)
        add(a[i].c, -1);
    sort(a + l, a + r + 1, comb); // 将该部分全部按b进行排序
}
// cdq分治主函数
void cdq(int l, int r)
{
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    cdq(l, mid);      // 左边去跑cdq分治
    cdq(mid + 1, r);  // 右边去跑cdq分治
    merge(l, mid, r); // 左右都跑完再进行左跨右贡献
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        cin >> a[i].a >> a[i].b >> a[i].c;
    sort(a + 1, a + n + 1, coma);
    // 以下为预贡献操作
    int cnt = 1;
    a[1].i = 1;
    for (int i = 2; i <= n; i++)
    {
        a[i].i = i;
        if (a[i] == a[i - 1])
            cnt++;
        else
        {
            for (int j = i - cnt; j < i; j++)
                f[j] += i - j - 1; // 加上后面所有相同元素的个数
            cnt = 1;
        }
    }
    for (int j = n - cnt + 1; j < n + 1; j++)
        f[j] += n - j;
    // 开始跑cdq分治，然后统计答案，输出答案。
    cdq(1, n);
    for (int i = 1; i <= n; i++)
        ans[f[i]]++;
    for (int i = 0; i < n; i++)
        cout << ans[i] << "\n";
}

​ 以上便是cdq分治的核心思想，面对一个多维问题时，应当如何逐步降维解决问题。但常常我们难以发现这是三维问题，下面我们具体问题具体分析。

eg1：动态逆序对

[P3157 CQOI2011] 动态逆序对 - 洛谷

问题简述：现在给出 1∼n 的一个排列，按照某种顺序依次删除 m 个元素，你的任务是在每次删除一个元素之前统计整个序列的逆序对数。

cdq分治的切入点： cdq分治的核心思想是将动态问题转化为静态问题。对于一个包含时间和修改操作的序列，我们可以把每个操作都看作一个事件，然后按时间顺序来处理。cdq分治通过对时间进行分治，可以巧妙地处理“一个修改对未来所有查询的影响”。

具体到这道题，我们可以把问题分解为两个部分：

  1. 初始状态下的逆序对数：这是个静态问题，可以用归并排序或树状数组轻松解决。
  2. 每次修改带来的逆序对数的增量：这是动态部分，也是cdq分治要解决的核心。总的逆序对数就是初始逆序对数加上所有增量的累加和。

所以，我们的目标就是计算出每一次操作事件所引起的逆序对数量的变化量。

那么每个增加/删除事件应当有4个属性：时间，操作属性（增加/删除），增加/删除的值，值的原始序列。

请自行思考该如何转化为三维问题：大顺序应当取什么，分治内顺序应当如何，树状数组记录的数据应当是什么。

eg2：序列

[P4093 HEOI2016/TJOI2016] 序列 - 洛谷

问题简述：给定一个长度为n的数列，以及m个可能的单点修改操作。要求你从原数列中选择一个最长的子序列，使得无论这m个修改中的任意一个是否发生，这个子序列都是不降的。输出这个最长不降子序列的长度。

注意：修改只会取其中任意一个或者不发生。

分析：

这很明显是dp问题，对于每一个单点，应当有三个值：原始值v，所能到达的最大值vr，所能到达的最小值vl。

假设我们有两个点 ai 和 aj ，在什么情况下，dp[i]可以等于dp[j]+1？

  1. j<i;
  2. 如果当前点发生了修改，那么它不管怎么改，都应当是大于等于v[j]的，也就是vl[i]>=v[j];
  3. 如果j点发生了修改，那么它不管怎么改，都应当是小于等于v[i]的，也就是vr[j]<=v[i];

对于每一个i,我们都想找到最大的符合条件的dp[j],我们可以对树状数组的功能进行修改，将其功能变为求前缀最大值，具体如何修改请自行学习树状数组。

该问题的关键已经讲完。

请自行思考该如何转化为三维问题：大顺序应当取什么，分治内顺序应当如何，树状数组记录的数据应当是什么。

注：分治内顺序左右组的参照值可不同。

Prev
2025-08-22 19:10:29 # code